Tychonoff plank

In topology, the Tychonoff plank is a topological space that is a counterexample to several plausible-sounding conjectures. It is defined as the product of the two ordinal space

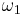$[0,\omega_1]\times[0,\omega]$

where $\omega$ is the first infinite ordinal and $\omega_1$ the first uncountable ordinal.

The deleted Tychonoff plank is obtained by deleting the point 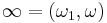$\infty = (\omega_1,\omega)$ .

The Tychonoff plank is a compact Hausdorff space and is therefore a normal space. However, the deleted Tychonoff plank is non-normal. Therefore the Tychonoff plank is not completely normal. This shows that a subspace of a normal space need not be normal. The Tychonoff plank is not perfectly normal because it is not a Gδ space: the singleton 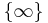$\{\infty\}$ is closed but not a Gδ set.

References

Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-486-68735-3, MR 507446

External links

Barile, Margherita, "Tychonoff Plank" from MathWorld.